হ্যানয় শহরটা ভিয়েতনামে। সেখানে পুরোনো টাওয়ার আছে বটে। তবে তা নিয়ে আর বলার কি আছে! অবশ্য আজকালকার দিনের উঁচু উঁচু আকাশছোঁয়া বাড়িগুলোকেও টাওয়ার বলে। তো, তাতেই বা কি?

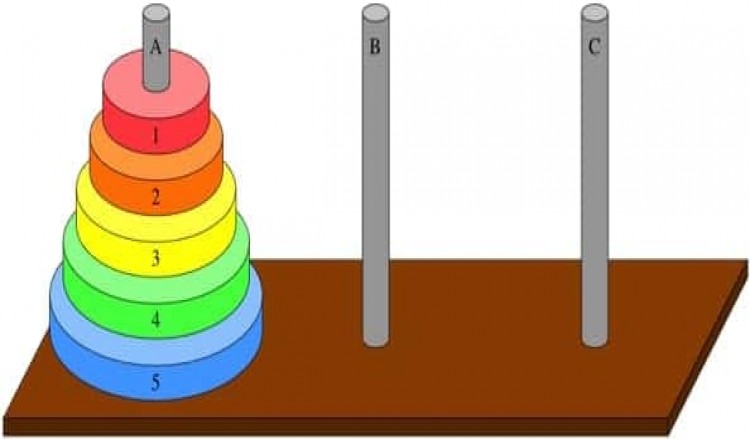
আসলে টাওয়ার অব হ্যানয় (Tower of Hanoi) হলো একটা মজার খেলা। ছোটোবেলায় অনেকেই হয়ত খেলেছি। খেলনার দোকানে খোঁজ করলে পাওয়া যাবে। তিনটে কাঠি বা প্লাস্টিকের দন্ড আর কতগুলো প্লাস্টিকের রিং। নিজেরাও কিছু দিয়ে বানিয়ে নিতে পারো এটা ওটা দিয়ে। মনে করা যাক, দন্ডগুলো পরপর এক লাইনে দাঁড় করানো। একটা দন্ডের মধ্যে সব রিংগুলো একটার পর একটা ঢোকানো আছে বড় থেকে ছোটো। সবচেয়ে নীচে সবচেয়ে বড় রিং, তার উপর তার থেকে ছোটো, তারও উপর তার থেকে ছোটো...এইভাবে সবচেয়ে উপরে সবচেয়ে ছোটো রিং। দেখতে হবে একটা শঙ্কু বা পিরামিডের স্টাইলে। খেলাটা হলো, এই রিংগুলো কে একটা একটা করে নিয়ে অন্য খালি দন্ডগুলোর কোনো একটাতে আবার এভাবেই সাজিয়ে রাখতে হবে। তবে, কোনো অবস্থাতেই একটা রিং-এর উপর তার থেকে বড় কোনো রিং রাখা যাবে না। আর, যে কোনো অবস্থায় সবচেয়ে উপরের রিংটাই তো বার করতে পারবে। একটা একটা করেই বার করতে হবে। (ছবি নীচে আছে। নেট সার্চ করলেও দেখতে পাবে।)

কল্পনা করে নাও, বাঁদিক থেকে ধরলে, প্রথম দন্ড টা ভর্তি, তারপর দ্বিতীয় ও তৃতীয় দন্ড খালি। তুমি তিন নম্বর দন্ডটার ভিতরে এই রিংগুলোকে, যেমন বলা হয়েছে, সেরকম পর পর সাজিয়ে রাখতে চাও। হয়ত তিনটে, চারটে, পাঁচটা বা যত খুশী রিং নিয়ে এই খেলাটা খেলছো। রিং এর বদলে ডিস্ক হলেও ব্যাপারটা একই। একটু খেয়াল করে দ্যাখো, একবারে তো কখনোই রাখতে পারবে না। তোমাকে দ্বিতীয় দন্ডটার সাহায্য নিতেই হবে। রিংগুলো কে কিন্তু আলাদা করে এদিক ওদিক, মেঝেতে রাখা যাবে না, কোনো না কোনো দন্ডের মধ্যে রাখতেই হবে!

মনে করা যাক, দুটো রিং আছে। তাহলে তো খুব সোজা। উপরের ছোটো টা মাঝখানের (দ্বিতীয়) দন্ডের ভিতর তুলে রাখলে। এটা হলো প্রথম স্টেপ। তারপর বড় টা তুলে তিন নম্বর (সবচেয়ে ডানদিকে) টা তে রাখলে। এটা হলো তোমার দ্বিতীয় স্টেপ। এরপর মাঝখানেরটা তে রাখা ছোটো রিং টা কে আবার তুলে তৃতীয় দন্ডে বড় টার উপর রাখলে। ব্যাস! তোমার কাজ শেষ। তাহলে কটা স্টেপ হলো? সব মিলিয়ে তিনটে স্টেপ।
বেশ সোজা ব্যাপার!

কিন্তু, ব্যাপারটা হলো, এবার তুমি দুটো রিং এর বদলে তিনটে রিং নিয়ে খেলতে চাও। একটু জটিল হবে। হিসেব করে দ্যাখো, কমপক্ষে ৭ টা স্টেপ লাগবেই।
চেষ্টা করে দ্যাখো। তবে, আমি একটা সমাধান বলছি।
১. উপরের সবচেয়ে ছোটো টা তিন নম্বর দন্ডে।
২. এরপর মাঝারি টা মাঝের দু নম্বর দন্ডে।
৩. এবার তিন নম্বর থেকে ছোটো টা মাঝখানে আনলে।
৪. এবার এক নম্বর থেকে সবচয়ে বড়টা তিন নম্বরে।
৫. এরপর মাঝের দন্ডের উপরের ছোটো টা আবার এক নম্বরে এনে রাখো।
৬. এবার মাঝের দন্ডের ভিতরে রাখা মাঝারি রিং টা তিন নম্বরে বড়টার উপর চাপাও।
৭. এইবার প্রথম দন্ডে রাখা সবচেয়ে ছোটো রিং টা তিন নম্বর দন্ডে রাখো।

দ্যাখো, হলো কিনা! চেষ্টা করতে পারো, এর থেকে কম সংখ্যক স্টেপে করা যায় কিনা।

আসলে, অঙ্ক করে দেখানো যেতে পারে, এর থেকে কম স্টেপে করা সম্ভব নয়!

এমনিতে হিসেব রাখা খুব কঠিন। যত রিং এর সংখ্যা বাড়তে থাকবে, তত খেলাটা ঝপ করে জটিল, তস্য জটিল হতে থাকবে। আর তেমনি সময়ও লাগবে সমাধানে পৌঁছাতে। তবে, এখানেই তো খেলাটার মজা। এটা একটা দারুণ সহজ খেলা কিন্তু জমাটি ধাঁধার মতো। এরকম একটা খেলনা বাড়িতে থাকলে, বা বানিয়ে নিলে তা নিয়ে বেশ সময় কেটে যাবে! রিং এর বদলে চাকতি বা কৌটোর ঢাকনা, প্লাস্টিকের বোতলের ক্যাপ ইত্যাদি দিয়ে ব্যাপারটা রেডি করে ফ্যালো। প্রথমে তিনটে, পরে চারটে, পাঁচটা....!

তবে, খেলার মজা যেমন আছে, তার থেকেও বড় কথা হলো, আমাদের খুব শান্ত হয়ে ভাবার একটা চাহিদা থাকবে, যাকে বলে mental discipline বা discipline of thought!
এই গেমটা কে মনস্তত্ববিদরা (psychologists) প্রায়ই ব্যবহার করেন বাচ্চাদের চিন্তার গঠন (cognitive ability) বোঝার জন্য। অনেক আধুনিক স্কুলে বাচ্চাদের কে এই গেম টা বা এধরণের আরো কিছু গেম দেওয়া হয় তাদের যুক্তি-চিন্তার বিকাশে যাতে সাহায্য হয়।

তবে তুমি যদি খুব ভালো করে খেয়াল রাখো, হিসেব করে বার করে ফেলতে পারবে, যে, কটা রিং নিলে নূন্যতম কতগুলো স্টেপ দরকার হবে সমাধানে পোঁছতে।
যেমন ধরো, একটা রিং নিলে একটা স্টেপেই করে ফেলবে। দুটো রিং নিলে ৩ টে স্টেপ লাগবে, তিনটে রিং নিলে ৭ টা স্টেপ লাগবে...
কিছু কি একটা মিল আছে? কোনো ফর্মূলা কি বার করা যায়?

সাংকেতিক ভাষায় লেখা যাক।
T1 = 1
T2 = 3
T3 = 7
.....
আবার দ্যাখো T0 = 0. মানে হলো, তুমি যদি জিরো রিং নাও তো জিরো উত্তর হবে! এটা একেবারেই ছেলেভোলানো ব্যাপার হলেও, অঙ্কের যুক্তির কাছে অবশ্য কিছুই ফেলনা নয়।

যাই হোক, এবার দেখা যাক, এসব টার্মগুলোর মধ্যে কোনো সম্পর্ক আছে কিনা!
একটু মাথা খাটালেই দেখতে পাবে,

T1 = 2×T0 1 = 2×0 1 = 1
T2 = 2×T1 1 = 2×1 1 = 3
T3 = 2×T2 1 = 2×3 1 = 7

এভাবে চলতে থাকলে আমরা কি বলতে পারি, T4 = 2×T3 1 = 2×7 1 = 15? অর্থাৎ ৪ টে রিং নিয়ে খেললে কমপক্ষে ১৫ টা স্টেপ বা চাল লাগবে?
তাহলে কি আরো সাধারণভাবে বলা যায়, যে কোনো সংখ্যক রিং, ধরা যাক n সংখ্যক রিং-এর ক্ষেত্রে একইভাবে হিসেব টা (n-1) সংখ্যক রিং নিয়ে খেললে যা হয় তার সাহায্যে উপরের ঐ একই সম্পর্ক দিয়ে পাওয়া যাবে?

কিন্তু ফর্মূলা টা আসলে কি, যা দিয়ে জানা যাবে কতগুলো রিং এর জন্য নূন্যতম কতগুলো স্টেপ দরকার হবে?

এবার একটা অনুমান করা যেতে পারে।
একটু সংখ্যাগুলোর দিকে তাকিয়ে দ্যাখো,

1 = 2×1 - 1 = 2^1 - 1
3 = 2×2 - 1 = 2^2 - 1
7 = 2×2×2 - 1 = 2^3 - 1

[এখানে, 2^3 হলো 2 to the power 3 ইত্যাদি।]

বেশ! তা যদি হয়, তাহলে একটা সাধারণ বা জেনারেল ফর্মূলা হতে পারে,
Tn = 2^n - 1
এই ফর্মূলা টা সত্যি কিনা, তার মানে হলো, ফর্মূলা টা বরাবর n = 0, 1, 2, 3, 4, 5, 6...ইত্যাদি যে কোনো ভ্যালুর জন্য খাটবে কিনা তা খতিয়ে দেখার জন্য তা আগের ওই রিলেশনে বসিয়ে দ্যাখো।

T2 = 2×T1 1 = 2×(2^1 -1) 1 = 3
T3 = 2×T2 1 = 2×(2^2 -1) 1 = 7
T4 = 2×T3 1 = 2×(2^3 -1) 1 = 15

এইরকম ব্যাপার। এবারে, একেবারে, সাংকেতিক বীজগণিতের ফর্মূলা লিখে ফেলতে পারো n-th টার্মের ফর্মূলা টা নিশ্চই 2^n - 1 হবে আর তার সাথে তার ঠিক আগের টার্মের সম্পর্কও নিশ্চই সেইরকম হবে, যা প্রথমে হিসেব করা হলো। এই যে n-th term এর সাথে (n-1)th term এর সম্পর্ক বা রিলেশান টা খাতায় লিখলে, এ ধরণের রিলেশান কে অঙ্কের ভাষায় বলে রিকার্শান রিলেশান (recursion relation), মানে হলো, একটা integer value এর জন্য কিছু জানা থাকলে তা থেকে তার পরের কোনো integer value এর জন্য মান বের করে ফেলা! অঙ্কে এর অজস্র উদাহরণ আছে। আর মজা হল, এরকম একটা relation জানা থাকলে, আর প্রাথমিক ভাবে দু একটা কেস হিসেব করে ফেলতে পারলে, তা দিয়ে পটাপট পরবর্তী যে কোনো ভ্যালুর জন্য মান জানা যাবে!
আর এই যে প্রথমে 0, 1, 2..এর কেসগুলো হাতে করে হিসেব করে তা থেকে পরবর্তী যে কোনো বড় ভ্যালুর জন্য মান বের করার ফর্মূলা বার করা হলো, এই পদ্ধতি কে অঙ্কের ভাষায় বলে Mathematical Induction!

এবার তুমি নিশ্চিত, যে কোনো সংখ্যক রিং দিয়ে খেলাটা খেলতে বললে, তোমার একটা আইডিয়া থাকবে, নূন্যতম কতগুলো স্টেপ লাগবে। যেমন ধরো, দোকানে যে Tower of Hanoi খেলনা পাওয়া যায়, তাতে মোটমুটি 5 টা রিং থাকে, তার মানে হলো, অন্ততপক্ষে 2^5 - 1 = 31 সংখ্যক স্টেপ লাগবে সমাধানে পৌঁছাতে।

তবে খেলতে পারা বা সমাধানে পৌঁছানোর রাস্তাটা কিন্তু অত সহজ নয়। বেশী সংখ্যক রিং এর জন্য খেলতে গেলে বেশ চিন্তাভাবনা করে এগোতে হবে। বুদ্ধিতে শাণ দিতে হবে বৈকি! যদিও তুমি অঙ্কের ফর্মূলা দিয়ে চট করে হিসেব করে জেনে নেবে কমপক্ষে কতগুলো চাল দিতে হবে!
এই খেলাটার আবার অনেক রকমফের (variation) আছে। গণিতজ্ঞরা মাথা খাটিয়ে নানারকম পরিবর্তন এনেছেন, তাঁদের অঙ্ক নিয়ে নানারকম পরীক্ষানিরীক্ষার জন্য। গণিতের ওই বিশেষ শাখা কে বলে Discrete Mathematics, যার সাথে কম্পিউটার সায়েন্সের খুব আত্মিক যোগাযোগ! মানে হলো, কম্পিউটার কে দিয়ে কাজ করিয়ে নিতে গেলে, কঠিন সব অঙ্ক বা সমস্যার সমাধান করাতে গেলে তার আগে এই discrete mathematics এর সাহায্য নিতে হয়।

খুব সুন্দর সুন্দর বই আছে, বড় হয়ে পড়বে। এই যেমন 'Concrete Mathematics' by Graham, Knuth & Patashnik. আহা! একেবারে কবিতার মত করে যেন লেখা। আর হবে নাই বা কেন! এনারা যে বিশ্বের নামকরা বিশ্ববিদ্যালয় বা রিসার্চ ল্যাবোরেটরির অধ্যাপক বা বিজ্ঞানী তা তো শুধু নয়, অসম্ভব ভালোবাসা আর নিষ্ঠা লেগে আছে যেন পাতায় পাতায়!

এই যাঃ! কথা বলতে বলতে বেশ খানিকটা অঙ্কের কারবার হয়ে গেলো! আসলে কি জানো, অঙ্ক তো আর শুধু কতগুলো সংখ্যা বা সাংকেতিক কিছু লিখে হিসেবনিকেশ করে যাওয়া নয়! অঙ্কের ভিতর দিয়ে বেরিয়ে আসে জীবনের অনেক কিছু ভাবনা, যাকে গুরুগম্ভীর ভাষায় বলে জীবন দর্শন!
যেমন ভাবতে পারো, Mathematical Induction একটা সুন্দর দর্শন। জীবনে যখনই কোনো কঠিন জটিল সমস্যায় পড়বে, কিছুতেই ভেবে কুলকিনারা করতে পারছো না, তখন একেবারে শূণ্য থেকে শুরু করো, একটু একটু করে এগোতে থাকো, স্টেপ বাই স্টেপ। একটা স্টেপ এগিয়ে তার সাথে আগের স্টেপের কি সম্পর্ক আছে তা ভাবার চেষ্টা করো। তারপর খানিকটা আন্দাজ করো, কি হতে পারে, তা আবার মেলাও যতটুকু এগিয়েছো তাই দিয়ে, দেখবে ফেলুদার মতো ঠিক পৌঁছে যাচ্ছো রহস্যের জাল উন্মোচনের দিকে!

এই যে একটা ছোট্ট গেম খেলা হলো, এটা বাচ্চাদের কাছে যেমন খুব প্রিয়, তেমনি, আগেই বলেছি, অঙ্কের লোকদের কাছেও এর গুরুত্ব অনেক। আবার কম্পুটার সায়েন্স নিয়ে পড়াশুনা করলে দেখতে পাবে কিভাবে তুমি তোমার লজিক বা যুক্তি লাগিয়ে এরকম একটা প্রবলেম কে সলভ করার জন্য কয়েকটা নির্দিষ্ট স্টেপ লিখে ফেলছো, যেগুলো সঠিক নিয়ম মেনে বার বার করলে তুমি খেলাটা অনায়াসে শেষ করতে পারবে। তুমি যদি রিংগুলোকে যেমন তেমন এদিক ওদিক না নিয়ে কিছু নির্দিষ্ট স্টেপ বা নিয়ম (method) অনুসরণ করতে থাকো তবে ঠিক সমাধানে পৌঁছবে, নূন্যতম স্টেপ ব্যবহার করেই। এই যে স্টেপগুলোর কথা বললাম, কম্পিউটারের ভাষায় এদের কে বলে Computer Algorithm (এলগোরিদম)। এগুলো থেকে এবার কম্পিউটারের কোনো language-এ (যেমন Fortran, C, C , Java, Python ইত্যাদি) একটা set of instructions অর্থাৎ কয়েকটা লাইন লিখে ফেললেই কম্পুউটার তোমার করার অনেক অনেক আগে, অত্যন্ত দ্রুত নিশ্চিত সমাধান করে ফেলবে!

যাই হোক, এসব নিয়ে অনেক কিছু বলা যাবে আরেকদিন। এবার বলি এই গেমটার এরকম নাম কেনো। আর, তারপর জানবে আরো অনেক রহস্য জড়িয়ে আছে এর সাথে।

এদুয়ার্ড লুকাস (Eduard Lucas) নামের একজন ফরাসী গণিতজ্ঞ এই গেম টার কথা ইউরোপের লোকদের কে জানান ১৮৮৩ সালে, আর এ নিয়ে অঙ্ক করেন। তখন ভিয়েতনাম ছিল ফরাসীদের অধীনে, বলা যেতে পারে ফরাসী কলোনি। আসলে তখন জাপান, চীন, ভিয়েতনাম - এশিয়ার এই দেশগুলোতে এই ধরণের একটা গেম এর কথা লোকে জানতো। লুকাস নিশ্চই তার সন্ধান পেয়ে তার থেকে গেমটার মজা টা অঙ্কের সাহায্যে বোঝার চেষ্টা করেন। তাই নাম দিয়ে দিলেন ভিয়েতনামের হ্যানয় টাওয়ারের নামে (Tower of Hanoi)! সে নামেই বেশীরভাগ লোকে এখন জানে। অবশ্য কেউ কেউ Tower of Lucas ও বলে।

কিন্তু, জানা গেলো, এই গেমটা অনেক অনেক পুরোনো, যাকে বলে একেবারে পুরাণের যুগের। আমাদের দেশেই এই গেম এর সৃষ্টি! পুরাণে কোথাও নিশ্চয়ই এর উল্লেখ আছে। হিন্দু শাস্ত্রে অথবা লোকের মুখে মুখে, কিভাবে তার অস্তিত্ব ছিলো তা গবেষণার বিষয়। এর আসল ও আদি নাম হলো, Tower of Brahma! ব্রহ্মার টাওয়ার বলতে পারো।

এখানে ওখানে, এমনকি অনেক অঙ্কের বই বা ইন্টারনেট, যেখানেই এই গেম টা নিয়ে বলা আছে, উল্লেখ আছে, ভারতের কোনো মন্দিরে নাকি তিনটে বিশেষ স্তম্ভ আছে আর আছে ৬৪ টা সোনার ডিস্ক (Golden disc)! ব্রাহ্মণ পুরোহিতদের নাকি পৌরাণিক নির্দেশ অনুযায়ী এই ৬৪ টা সোনার ডিস্ক কে এরকম গেমের নিয়ম মেনে একটা অন্য স্তম্ভের ভিতর সাজাতে হবে। তাঁরা নাকি নিরন্তর চেষ্টা চালিয়ে যাচ্ছেন, অদৃশ্য কারো নির্দেশ মেনে, যুগ যুগ ধরে। এখনো সফল হন নি। কবে হবে কেউ জানে না!

Tower of Brahma নিয়ে লেখা আছে বিখ্যাত নোবেলজয়ী রাশিয়ান বিজ্ঞানী জর্জ গ্যামো (George Gamow)-এর বই 'One Two Three...Infinity' তে। অসাধারণ একটা বই। তোমাদের জন্যই লেখা। সুযোগ পেলে, পড়ে দেখতে পারো। বলা আছে বারাণসী (Benares) তে কাশী বিশ্বনাথ মন্দিরের ভিতর একটা জায়গায় ('beneath the Dome'), যেখানটা পৌরাণিক মতে পৃথিবীর কেন্দ্রবিন্দু বলে ভাবা হতো, একটা ব্রোঞ্জ পাতের উপর বসানো আছে তিনটে হীরের সরু দন্ড। বিশ্ব সৃষ্টির শুরুতে ভগবান ব্রহ্মার নির্দেশে একটা দন্ডের ভিতর ৬৪ টা সোনার ডিস্ক (disc), নীচের দিক থেকে বড় থেকে ছোটো, সাজানো ছিল। পুরোহিতরা ব্রহ্মার নির্দেশ মেনে যুগযুগান্ত ধরে দিনরাত চেষ্টা করে যাচ্ছেন কিভাবে ওই ৬৪ টা ডিস্ক অন্য একটা দন্ডের ভিতরে ঢুকিয়ে ঠিক ঐ একই অর্ডারে সাজিয়ে রাখা যায়!

অবশ্য গল্পের এখানেই শেষ নয়। বলা আছে যেদিন এই কাজ শেষ হবে, সেদিন এই মহাবিশ্ব ধ্বংস হয়ে যাবে! কী সাংঘাতিক ব্যাপার ভাবো!

গ্যামো-এর বইতে বা অন্য অনেক জায়গাতেই এই গল্পটা প্রায় এরকমই বলা আছে। পৌরানিক কাহিনীর তো আর কোনো ঐতিহাসিক ভিত্তি হয় না, তা শুধু কল্পনা নির্ভর। হয়ত অতিরঞ্জিত বর্ণনা আছে বইতে। কাশীর বাবা বিশ্বনাথের মন্দিরে ঢুকে একবার খোঁজ করতেই হবে দেখছি!

তবে, এমন বাহাদুরি ভাবনা, এমন একটা খেলার উৎপত্তি থেকে বোঝা যায় সে যুগের মানুষদের কল্পনাশক্তি কত প্রবল ছিল! হয়ত হিন্দু পুরোহিতদের থেকে সাধারণ মানুষের হাত ধরে বৌদ্ধ ধর্মপ্রচারকদের মাধ্যমে তা এশিয়ার বিভিন্ন জায়গায় পৌঁছেছিলো। তারপর লোকমুখে, মানুষের জীবনে এই খেলার চল থেকে যায়। এরপর সেই ফরাসী গণিতজ্ঞ লুকাসের হাত ধরে ইউরোপ পোঁছায়! তারপর সারা দুনিয়ার মানুষ, গণিতজ্ঞ, বিজ্ঞানী বা সাধারণ মানুষ, বাচ্চা ছেলেমেয়েরা, সবাই এখন এই খেলা টা জানে। এই খেলা বা গেম নানা বইতে স্থান পেয়েছে, এ থেকে অঙ্ক ও কম্পিউটার সায়েন্সের নানা কিছুর সমস্যার সমাধানের রাস্তা পরিষ্কার হয়েছে, আর, হাজার হাজার বছর পাড়ি দিয়ে আমরা এখনো এ নিয়ে আলোচনা করে চলেছি।

আচ্ছা, সত্যি কি তাহলে ওই পুরোহিতদের নিরলস প্রচেষ্টা সফল হবে? সত্যি কি সমাধান করতে পারবেন ওনারা আর মহাবিশ্ব সেদিন ধ্বংস হয়ে যাবে? একটা ছোটো হিসেব তো অন্তত করে দেখা যাক! কেননা, ফর্মূলা তো আমরা আগেই বের করে ফেলেছি। মানে, অন্ততপক্ষে কতবার ওই সোনার ডিস্ক গুলোকে সরাতে হবে সেটা একবার দেখে নিই।

হিসেব টা হলো,

2^64 - 1 = 18446744073709551615

উপরের সংখ্যায় কতগুলো ঘর, মানে কত বড় সংখ্যা সেটা নিজে গুণে দ্যাখো, আমার মাথা ঘুরে যাচ্ছে! কিন্তু ব্যাপারটা হলো, ধরো একটা ডিস্ক এই দন্ড থেকে ওই দন্ডে নিয়ে যেতে ১ সেকেন্ড সময় লাগছে, তাহলে অত সেকেন্ড সময় তো লাগবেই! এবার তাহলে মিনিট, ঘণ্টা, দিন, বছর হিসেব করে ফ্যালো একটা ক্যালকুলেটর নিয়ে। মানে, ওই সংখ্যা টা কে ভাগ করতে হবে (60×60×24×365) দিয়ে, তবে কত বছর লাগবে তা জানা যাবে (তাও সেটা নূন্যতম)।

হিসেব টা দাঁড়ালো 584942417355 বছর। তার মানে, 58494 কোটি বছরের ও বেশী। আন্তর্জাতিক পদ্ধতিতে হিসেব করলে প্রায় ৫৮৫ বিলিয়ন ইয়ার (Billion year, 1 billion = 1000, 000, 000)! এদিকে আমাদের এই মহাবিশ্বের (Universe) বয়সই তো হলো এখন পর্যন্ত মাত্র 13.8 বিলিয়ন ইয়ার! অবশ্য আরো বেশ কয়েক বিলিয়ন ইয়ার তো তা টিঁকবেই! আর পৃথিবীর বয়স তো আরো কম, মাত্র 4.5 বিলিয়ন ইয়ার। হয়ত আরো অত দিন পৃথিবী বেঁচে থাকবে, অর্থাৎ যদি ধরে নেওয়া যায় পৃথিবীর বয়স মধ্যগগণে। তবুও, ওই ডিস্কগুলো নির্দেশ মেনে ঠিক করে রাখতে কমপক্ষে 585 বিলিয়ন ইয়ার যদি লাগে, তো, তার মধ্যে হয়ত কতবার, আরো কত মহাবিশ্ব সৃষ্টি হবে আর ধ্বংস হবে কে জানে! যাই হোক, ব্রহ্মা যে কত ভয়ংকর কঠিন এক প্রবলেম দিয়েছিলেন তা তো বোঝাই যাচ্ছে!